Neural Networks

Number of Training Epochs¶

A training epoch refers to one sweep through the entire training set.

From Neural Networks Part 3: Learning and Evaluation

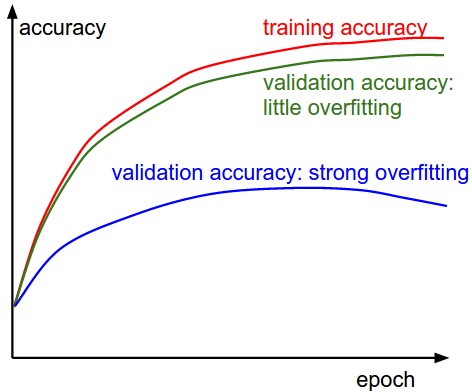
Two possible cases are shown in the diagram on the left. The blue validation error curve shows very small validation accuracy compared to the training accuracy, indicating strong overfitting (note, it's possible for the validation accuracy to even start to go down after some point). When you see this in practice you probably want to increase regularization (stronger $L2$ weight penalty, more dropout, etc.) or collect more data. The other possible case is when the validation accuracy tracks the training accuracy fairly well. This case indicates that your model capacity is not high enough: make the model larger by increasing the number of parameters.

Number of Hidden Units and Layers¶

From Elements of Statistical learning

Generally speaking it is better to have too many hidden units than too few. With too few hidden units, the model might not have enough flexibility to capture the nonlinearities in the data; with too many hidden units, the extra weights can be shrunk toward zero if appropriate regularization is used. Typically the number of hidden units is somewhere in the range of 5 to 100, with the number increasing with the number of inputs and number of training cases. It is most common to put down a reasonably large number of units and train them with regularization. Some researchers use cross-validation to estimate the optimal number, but this seems unnecessary if cross-validation is used to estimate the regularization parameter. Choice of the number of hidden layers is guided by background knowledge and experimentation. Each layer extracts features of the input for regression or classification. Use of multiple hidden layers allows construction of hierarchical features at different levels of resolution.

Convolutional Networks¶

See layer sizing patterns for information on the number of layers for convolutional networks.

From Neural Networks Part 1: Setting up the Architecture

To give you some context, modern Convolutional Networks contain on orders of 100 million parameters and are usually made up of approximately 10-20 layers (hence deep learning). However, as we will see the number of effective connections is significantly greater due to parameter sharing.

From Convolutional Neural Networks

In practice: use whatever works best on ImageNet. If you’re feeling a bit of a fatigue in thinking about the architectural decisions, you’ll be pleased to know that in 90% or more of applications you should not have to worry about these. I like to summarize this point as “don’t be a hero”: Instead of rolling your own architecture for a problem, you should look at whatever architecture currently works best on ImageNet, download a pretrained model and finetune it on your data. You should rarely ever have to train a ConvNet from scratch or design one from scratch.

From Deep Residual Learning for Image Recognition

Exploring Over 1000 layers. We explore an aggressively deep model of over 1000 layers. We set n = 200 that leads to a 1202-layer network, which is trained as described above. Our method shows no optimization difficulty, and this 103-layer network is able to achieve training error <0.1% (Fig. 6, right). Its test error is still fairly good (7.93%, Table 6).

But there are still open problems on such aggressively deep models. The testing result of this 1202-layer network is worse than that of our 110-layer network, although both have similar training error. We argue that this is because of overfitting. The 1202-layer network may be unnecessarily large (19.4M) for this small dataset. Strong regularization such as maxout [10] or dropout [14] is applied to obtain the best results ([10, 25, 24, 35]) on this dataset. In this paper, we use no maxout/dropout and just simply impose regularization via deep and thin architectures by design, without distracting from the focus on the difficulties of optimization. But combining with stronger regularization may improve results, which we will study in the future.

From Neural Networks Part 1: Setting up the Architecture

The takeaway is that you should not be using smaller networks because you are afraid of overfitting. Instead, you should use as big of a neural network as your computational budget allows, and use other regularization techniques to control overfitting.

Densely Connected Networks¶

From Neural Networks Part 1: Setting up the Architecture

As an aside, in practice it is often the case that 3-layer neural networks will outperform 2-layer nets, but going even deeper (4,5,6-layer) rarely helps much more. This is in stark contrast to Convolutional Networks, where depth has been found to be an extremely important component for a good recognition system (e.g. on order of 10 learnable layers). One argument for this observation is that images contain hierarchical structure (e.g. faces are made up of eyes, which are made up of edges, etc.), so several layers of processing make intuitive sense for this data domain.

Large Number of Categories¶

From Elements of Statistical learning

With $N$ observations, $p$ predictors,$M$ hidden units and $L$ training epochs, a neural network fit typically requires $O(NpML)$ operations.

From Neural Networks Part 2: Setting up the Data and the Loss

Problem: Large number of classes. When the set of labels is very large (e.g. words in English dictionary, or ImageNet which contains 22,000 categories), computing the full softmax probabilities becomes expensive. For certain applications, approximate versions are popular. For instance, it may be helpful to use Hierarchical Softmax in natural language processing tasks (see one explanation here (pdf)). The hierarchical softmax decomposes words as labels in a tree. Each label is then represented as a path along the tree, and a Softmax classifier is trained at every node of the tree to disambiguate between the left and right branch. The structure of the tree strongly impacts the performance and is generally problem-dependent.

Dropout and Regularization¶

From Neural Networks Part 1: Setting up the Architecture

. . . there are many other preferred ways to prevent overfitting in Neural Networks that we will discuss later (such as L2 regularization, dropout, input noise). In practice, it is always better to use these methods to control overfitting instead of the number of neurons.

To reiterate, the regularization strength is the preferred way to control the overfitting of a neural network.

From Neural Networks Part 2: Setting up the Data and the Loss

In practice: It is most common to use a single, global L2 regularization strength that is cross-validated. It is also common to combine this with dropout applied after all layers. The value of p=0.5 is a reasonable default, but this can be tuned on validation data.

From Dropout: A Simple Way to Prevent Neural Networks from Overfitting

It is to be expected that dropping units will reduce the capacity of a neural network. If n is the number of hidden units in any layer and p is the probability of retaining a unit, then instead of n hidden units, only pn units will be present after dropout, in expectation. Moreover, this set of pn units will be different each time and the units are not allowed to build co-adaptations freely. Therefore, if an n-sized layer is optimal for a standard neural net on any given task, a good dropout net should have at least n=p units. We found this to be a useful heuristic for setting the number of hidden units in both convolutional and fully connected networks.

Hyperparameter Selection and Optimization¶

See hyperparameter optimization and Random Search for Hyper-Parameter Optimization for more information.

Here is a short excerpt:

Search for good hyperparameters with random search (not grid search). Stage your search from coarse (wide hyperparameter ranges, training only for 1-5 epochs), to fine (narrower rangers, training for many more epochs)

You can also look into tools like hyperopt